第六章-查找

平均查找长度：在查找过程中，一次查找的长度是指需要比较的关键字次数，而平均查找长度则是所有查找过程中进行关键字的比较次数的平均值：。其中n是查找表的长度；Pi是查找第i个数据元素的概率；Ci是找到第i个数据元素所需进行的比较次数。

顺序查找

• 一般线性表的顺序查找：从线性表的一端开始，逐个检查关键字是否满足给定的条件，引入哨兵的目的是使循环不必判断数组是否越界。当每个元素的查找概率相同时，
• 有序表的顺序查找：前提是线性表有序，

折半查找

int Binary_Search(SSTable L,ElemType key){
	int low=0,high=L.TableLen-1,mid;
	while(low<=high){                          
		mid = (low+high)/2;                    //取中间位置
		if(L.elem[mid]==key) return mid;       //查找成功则返回所在位置
		else if (L.elem[mid]>key) high=mid-1;  //从前半部分继续查找
		else low=mid+1;                        //从后半部分继续查找
	}
	return -1;                                 //查找失败，返回-1
}

折半查找可以使用二叉树进行描述，称为判定树。h是树的高度，并且元素个数为n是树高h= 所以

分块查找

将查找表分为若干个子块。块内元素可以无序，但块间的元素是有序的，即第一个块中的最大关键字小于第二个块中的所有记录的关键字，以此类推。再建立一个索引表，索引表中的每个元素含有各块的最大关键字和各块中的第一个元素的地址，索引表按关键字有序排列。
分块查找的平均查找长度为索引查找和块内查找的平均长度之和
将长度为n的查找表均匀地分为b块，每块有s个记录，在等概率情况下，若在块内和索引表中均采用顺序查找，则平均查找长度为

二叉排序树

1. 若左子树非空，则左子树上所有的结点值均小于根节点的值
2. 若右子树非空，则右子树上所有的结点值均大于根节点的值
3. 左、右子树也分别是一棵二叉排序树
   显然上述规则进行查找是个递归过程。
   从查找过程看，二叉排序树与二分查找相似。就平均性能而言，二叉排序树上的查找和二分查找差不多。但二分查找的判定树唯一，而二叉排序树的查找不唯一。

平衡二叉树（AVL）

规定在插入和删除结点时，要保证任意结点的左、右子树高度差的绝对值不超过1.
平衡二叉树的插入情况：

• LL（右单旋转）
• RR（左单旋转）
• LR（先左后右旋转）
• RL（先右后左旋转）

平均查找长度为O（）

红黑树

• 每个结点不是红色就是黑色
• 叶结点都是黑色的
• 根结点是黑色的
• 不存在相邻的红结点
• 对每个结点，从该结点到任意一个叶结点的简单路径上，所含黑结点的数量相同
• 从根到叶结点的最长路径不大于最短路径的2倍
• 有n个内部结点的红黑树高度
• 红黑树也是平衡二叉树

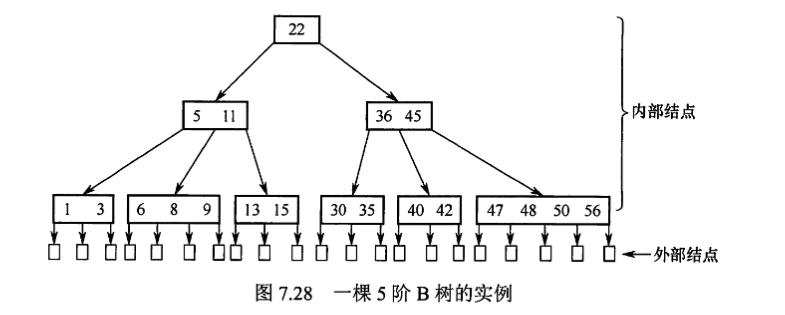
B树

m阶B树是所有结点的平衡因子均等于0的m路平衡查找树

• 树中每个结点至多有m棵子树，即至多含有m-1个关键字
• 若根结点不是叶结点，则至少有两棵子树
• 除根结点外的所有非叶结点至少有【m/2】棵子树，即至少含有【m/2】-1个关键字
• 所有的叶结点都有出现在同一层次上，并且不带信息
• B树的高度：
  
  B+树多出的特性：叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序相互连接起来

散列表

• 直接定址法：直接取关键字的某个线性函数值为散列地址
• 除留余数法
• 数字分析法
• 平方取中法：取关键字的中间几位做为散列地址

处理冲突的方法：

• 开放定址法：
  • 线性探测法：当di=0，1，2，···，m-1.会导致大量元素在相邻的散列地址上堆积起来，大大降低了查找效率
  • 平方探测法：当,m必须是可以表示为4k+3的素数
  • 双散列法：
  • 伪随机序列法
• 拉链法（可以随便删除链表中已有元素）